What is greatest common divisor, gcd code example
In mathematics, the greatest common divisor (gcd) of two or more integers, which are not all zero, is the largest positive integer that divides each of the integers.
The greatest common divisor (also known as greatest common factor, highest common divisor or highest common factor) of a set of numbers is the largest positive integer number that divides all the numbers in the set without remainder. It is the biggest multiple of all numbers in the set.
For example, the gcd of 8 and 12 is 4.
Formula to calculate
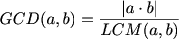
Problem
Write a java code that find the greatest common divisor for the two numbers.
Code
import java.util.Scanner;
public class GCD {
public static int gcd(int num1, int num2) {
if(num2 == 0) {
return num1;
}
return gcd(num2, num1%num2);
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
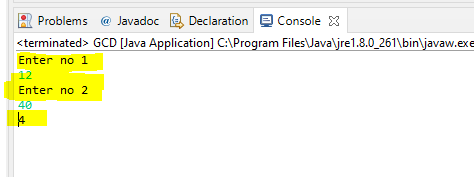
System.out.println("Enter no 1");
int n1 = scanner.nextInt();
System.out.println("Enter no 2");
int n2 = scanner.nextInt();
scanner.close();
System.out.println(GCD.gcd(n1, n2));
}
}
Run Code